Video: Wie beweist man, dass sich die Diagonalen einer Raute gegenseitig halbieren?
2024 Autor: Lynn Donovan | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:42
In einem Raute alle Seiten sind gleich und gegenüberliegende Seiten sind parallel. Weiter Rhombus ist ebenfalls ein Parallelgramm und besitzt daher Eigenschaften von a Parallelogramm und das Diagonalen eines Parallelogramms halbieren sich.
Halbieren sich dementsprechend die Diagonalen einer Raute?
In irgendeiner Rhombus , das Diagonalen (Linien, die gegenüberliegende Ecken verbinden) einander halbieren im rechten Winkel (90°). Das ist, jede Diagonale schneidet die Sonstiges in zwei gleiche Teile, und der Winkel, in dem sie sich kreuzen, beträgt immer 90 Grad. Ziehen Sie in der obigen Abbildung einen beliebigen Scheitelpunkt, um die Form zu ändern Rhombus und überzeugen Sie sich selbst, dass dies so ist.
Zweitens: Stehen Rhombusdiagonalen senkrecht? Eigenschaften von a Rhombus Die Diagonalen sind aufrecht zu und halbieren sich gegenseitig. Angrenzende Winkel sind ergänzend (zB ∠A + ∠B = 180°). EIN Rhombus ist ein Parallelogramm deren Diagonalen sind aufrecht zueinander.
Wenn man dies berücksichtigt, wie beweist man, dass die Diagonalen einer Raute senkrechte Winkelhalbierende sind?
Nachweisen dass die Diagonalen einer Raute sind senkrecht Fortsetzung oben nachweisen : Entsprechende Teile von kongruenten Dreiecken sind kongruent, also sind alle 4 Winkel (die in der Mitte) kongruent. Dies führt dazu, dass sie alle gleich 90 Grad sind und die Diagonalen sind aufrecht zueinander.
Ist Raute ein Parallelogramm?
DEFINITION: A Rhombus ist ein Parallelogramm mit vier deckungsgleichen Seiten. THEOREM: Wenn a Parallelogramm ist ein Rhombus , jede Diagonale halbiert ein Paar entgegengesetzter Winkel. THEOREM Umkehrung: Wenn a Parallelogramm Diagonalen hat, die ein Paar entgegengesetzter Winkel halbieren, ist a Rhombus.
Empfohlen:
Was ist eine Diagonale in einer Raute?
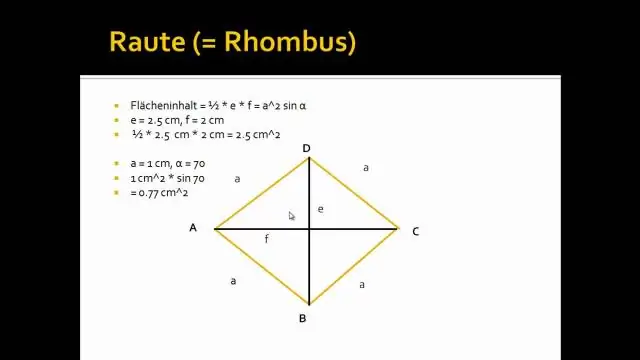
Diagonalen einer Raute In jeder Raute halbieren sich die Diagonalen (Linien, die gegenüberliegende Ecken verbinden) im rechten Winkel (90°). Das heißt, jede Diagonale schneidet die andere in zwei gleiche Teile, und der Winkel, in dem sie sich kreuzen, beträgt immer 90 Grad
Halbieren sich Diagonalen in einem Parallelogramm immer?
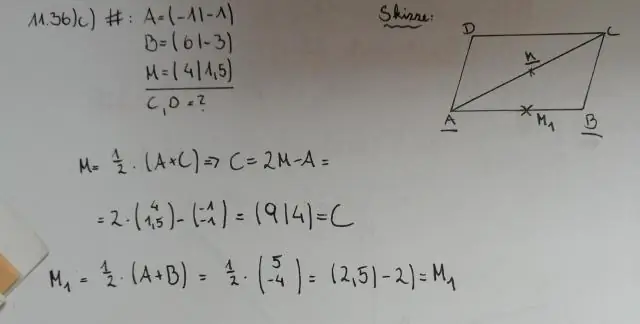
In jedem Parallelogramm halbieren sich die Diagonalen (Linien, die gegenüberliegende Ecken verbinden) einander. Das heißt, jede Diagonale schneidet die andere in zwei gleiche Teile. Ziehen Sie in der obigen Abbildung einen beliebigen Scheitelpunkt, um das Parallelogramm neu zu formen und sich selbst davon zu überzeugen, dass dies so ist
Halbieren sich Diagonalen des Parallelogramms bei 90?
In jeder Raute halbieren sich die Diagonalen (Linien, die gegenüberliegende Ecken verbinden) im rechten Winkel (90°). Das heißt, jede Diagonale schneidet die andere in zwei gleiche Teile, und der Winkel, in dem sie sich kreuzen, beträgt immer 90 Grad
Welche Parallelogramme haben Diagonalen, die sich gegenseitig halbieren?
Sind zwei benachbarte Seiten eines Parallelogramms gleich, handelt es sich um eine Raute. Dieser Test wird oft als Definition einer Raute angesehen. Ein Viereck, dessen Diagonalen sich im rechten Winkel halbieren, ist eine Raute
Wie beweist man einen linearen Code?
Ein linearer Code wird normalerweise als Unterraum von Fn für ein Feld F definiert (da Sie von Bits sprechen, können Sie F=F2={0,1} nehmen). Der von einer Generierungsmatrix G erzeugte Code C ist die Spanne der Zeilen von G. Die Spanne einer Menge von Vektoren in Fn ist ein Unterraum von Fn, also ist C ein linearer Code