Video: Welche Parallelogramme haben Diagonalen, die sich gegenseitig halbieren?
2024 Autor: Lynn Donovan | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:42
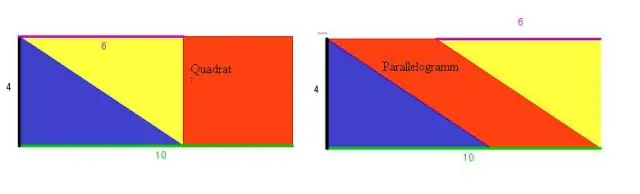
Wenn zwei benachbarte Seiten von a Parallelogramm sind gleich, dann ist es eine Raute. Dieser Test wird oft als Definition einer Raute angesehen. Ein Viereck, dessen Diagonalen halbieren sich im rechten Winkel ist eine Raute.
Haben alle Parallelogramme ebenfalls Diagonalen, die sich gegenseitig halbieren?
In irgendeiner Parallelogramm , das Diagonalen (Linien, die gegenüberliegende Ecken verbinden) einander halbieren . Das ist, jede Diagonale schneidet die Sonstiges in zwei gleiche Teile.
Wissen Sie auch, was die Diagonalen eines Parallelogramms sind? Die Diagonalen halbieren sich gegenseitig. Ein Paar gegenüberliegender Seiten ist parallel und gleich lang. Angrenzende Winkel sind ergänzend. Jeder Diagonale teilt das Viereck in zwei kongruente Dreiecke.
Wenn man dies berücksichtigt, halbieren sich Diagonalen des Parallelogramms bei 90?
Es ist ziemlich einfach zu beweisen, dass die Diagonalen von a Parallelogramm (und damit vom Besonderen Parallelogramm Rechteck genannt) einander halbieren . Ist der Winkel, in dem sie sich treffen, 90 ∘, dann nach dem Satz des Pythagoras jede einzelne Seite des Rechtecks hat die Länge √p2+q2.
Halbieren sich Diagonalen eines Trapezes?
Die Diagonalen einer gleichschenkligen trapezförmig sind auch deckungsgleich, aber sie tun NICHT einander halbieren . Gleichschenklig Trapezförmige Diagonalen Satz: The Diagonalen einer gleichschenkligen trapezförmig sind deckungsgleich. Das Mittelsegment (von a trapezförmig ) ist ein Liniensegment, das die Mittelpunkte der nicht parallelen Seiten verbindet.
Empfohlen:
Welche der folgenden Aussagen bezieht sich auf die Fähigkeit eines Computerprodukts oder -systems, sich zu erweitern, um eine größere Anzahl von Benutzern zu bedienen, ohne zusammenzubrechen?
Skalierbarkeit bezieht sich auf die Fähigkeit eines Computers, Produkts oder Systems, sich zu erweitern, um eine große Anzahl von Benutzern zu bedienen, ohne zusammenzubrechen. Die IT-Infrastruktur besteht nur aus den physischen Computergeräten, die für den Betrieb des Unternehmens erforderlich sind
Welche Wörter haben Mega in sich?
Wörter mit 8 Buchstaben, mit megabyte anfangen. Megawatt. Megastar. Megabock. Megalith. Megadosis. Megavolt. Megaflop
Halbieren sich Diagonalen in einem Parallelogramm immer?
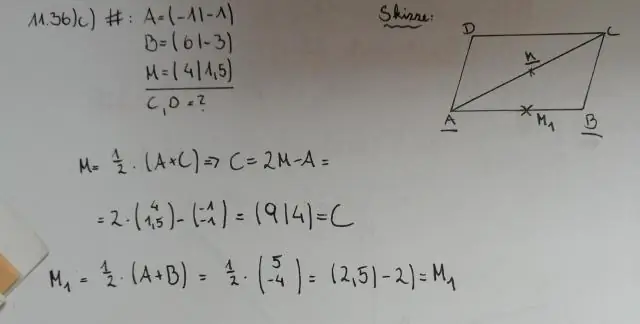
In jedem Parallelogramm halbieren sich die Diagonalen (Linien, die gegenüberliegende Ecken verbinden) einander. Das heißt, jede Diagonale schneidet die andere in zwei gleiche Teile. Ziehen Sie in der obigen Abbildung einen beliebigen Scheitelpunkt, um das Parallelogramm neu zu formen und sich selbst davon zu überzeugen, dass dies so ist
Halbieren sich Diagonalen des Parallelogramms bei 90?
In jeder Raute halbieren sich die Diagonalen (Linien, die gegenüberliegende Ecken verbinden) im rechten Winkel (90°). Das heißt, jede Diagonale schneidet die andere in zwei gleiche Teile, und der Winkel, in dem sie sich kreuzen, beträgt immer 90 Grad
Wie beweist man, dass sich die Diagonalen einer Raute gegenseitig halbieren?
Bei einer Raute sind alle Seiten gleich und gegenüberliegende Seiten sind parallel. Außerdem ist eine Raute auch ein Parallelogramm und weist daher Eigenschaften eines Parallelogramms auf und dass Diagonalen eines Parallelogramms sich halbieren