Video: Halbieren sich Diagonalen in einem Parallelogramm immer?
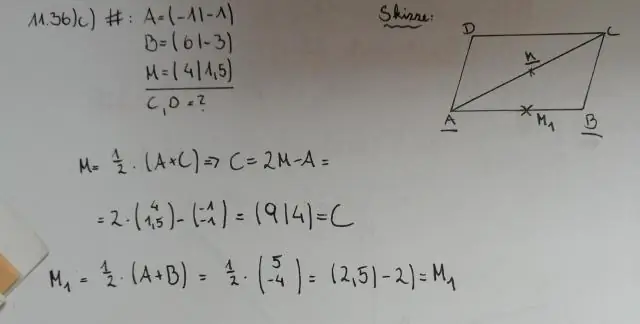
2024 Autor: Lynn Donovan | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:42
In irgendeiner Parallelogramm , das Diagonalen (Linien, die gegenüberliegende Ecken verbinden) einander halbieren . Das ist, jede Diagonale schneidet die Sonstiges in zwei gleiche Teile. Ziehen Sie in der obigen Abbildung einen beliebigen Scheitelpunkt, um die Form zu ändern Parallelogramm und überzeugen Sie sich selbst, dass dies so ist.
Wenn man dies im Auge behält, halbieren sich die Diagonalen des Parallelogramms bei 90?
In irgendeiner Rhombus , das Diagonalen (Linien, die gegenüberliegende Ecken verbinden) einander halbieren im rechten Winkel ( 90 °). Das ist, jede Diagonale schneidet die Sonstiges in zwei gleiche Teile, und der Winkel, in dem sie sich kreuzen, ist immer 90 Grad.
Anschließend stellt sich die Frage, welche Vierecke immer Diagonalen haben, die sich gegenseitig halbieren? Vierecke
| EIN | B |
|---|---|
| in diesen Vierecken sind die Diagonalen kongruent | Rechteck, Quadrat, gleichschenkliges Trapez |
| in diesen Vierecken halbiert jede der Diagonalen ein Paar entgegengesetzter Winkel | Raute, Quadrat |
| in diesen Vierecken stehen die Diagonalen senkrecht | Raute, Quadrat |
| eine Raute ist immer ein | Parallelogramm |
Anschließend stellt sich die Frage, welche Form Diagonalen hat, die sich nicht halbieren?
Da es sich bei der Frage um Diagonalen handelt, die sich halbieren, was effektiv bedeutet, dass sie sich in zwei Hälften schneiden, lautet die richtige Antwort auf die Frage D. Trapezoid , da die anderen in die Kategorie der Parallelogramme fallen, deren Diagonalen immer halbieren.
Stehen Parallelogrammdiagonalen senkrecht?
Die Diagonalen sind aufrecht zu und halbieren sich gegenseitig. Ein Quadrat ist eine besondere Art von Parallelogramm deren alle Winkel und Seiten gleich sind. Auch eine Parallelogramm wird ein Quadrat, wenn die Diagonalen sind gleich und rechtshalbierende zueinander.
Empfohlen:
Warum ordnen sich meine Desktopsymbole immer wieder neu an?
Wenn Windows Sie die Symbole nicht wie gewünscht neu anordnen lässt, ist höchstwahrscheinlich die Option „Symbole automatisch anordnen“aktiviert. Um diese Option anzuzeigen oder zu ändern, klicken Sie mit der rechten Maustaste auf eine leere Stelle Ihres Desktops und bewegen Sie den Mauszeiger, um das Element Ansicht im Kontextmenü zu markieren
Warum trennt sich mein Kindle Fire immer wieder vom WLAN?
Möglicherweise ist Ihr Router, der die drahtlose Verbindung bereitstellt, das Problem. Versuchen Sie, Ihren Kindle und Ihren Router neu zu starten. Wenn das Problem weiterhin besteht, haben Sie möglicherweise eine beschädigte Wireless-Platine, die ersetzt werden muss, oder Sie müssen sich zur weiteren Fehlerbehebung an Ihren Internetdienstanbieter wenden
Halbieren sich Diagonalen des Parallelogramms bei 90?
In jeder Raute halbieren sich die Diagonalen (Linien, die gegenüberliegende Ecken verbinden) im rechten Winkel (90°). Das heißt, jede Diagonale schneidet die andere in zwei gleiche Teile, und der Winkel, in dem sie sich kreuzen, beträgt immer 90 Grad
Welche Parallelogramme haben Diagonalen, die sich gegenseitig halbieren?
Sind zwei benachbarte Seiten eines Parallelogramms gleich, handelt es sich um eine Raute. Dieser Test wird oft als Definition einer Raute angesehen. Ein Viereck, dessen Diagonalen sich im rechten Winkel halbieren, ist eine Raute
Wie beweist man, dass sich die Diagonalen einer Raute gegenseitig halbieren?
Bei einer Raute sind alle Seiten gleich und gegenüberliegende Seiten sind parallel. Außerdem ist eine Raute auch ein Parallelogramm und weist daher Eigenschaften eines Parallelogramms auf und dass Diagonalen eines Parallelogramms sich halbieren