
- Autor Lynn Donovan [email protected].
- Public 2023-12-15 23:42.
- Zuletzt bearbeitet 2025-01-22 17:14.
EIN bedingte Wahrscheinlichkeit ist der Wahrscheinlichkeit dass ein Ereignis eingetreten ist, unter Berücksichtigung zusätzlicher Informationen über das Ergebnis des Experiments. Zwei Ereignisse A und B sind unabhängig wenn die Wahrscheinlichkeit P(A∩B) ihrer Schnittmenge A ∩ B ist gleich dem Produkt P(A)·P(B) ihres Individuums Wahrscheinlichkeiten.
Ist dies unter Berücksichtigung der bedingten Wahrscheinlichkeit abhängig?
Bedingte Wahrscheinlichkeit ist Wahrscheinlichkeit eines zweiten Ereignisses, wenn ein erstes Ereignis bereits eingetreten ist. Dies ist bedingte Wahrscheinlichkeit mit zwei abhängig Veranstaltungen. EIN abhängig Ereignis ist, wenn ein Ereignis das Ergebnis eines anderen Ereignisses in einem Wahrscheinlichkeit Szenario.
Wissen Sie auch, wie lautet die Formel für die bedingte Wahrscheinlichkeit von Ereignissen, die nicht unabhängig sind? In dem Fall, wo Veranstaltungen A und B sind unabhängig (wo Veranstaltung A hat Nein Wirkung auf die Wahrscheinlichkeit des Ereignisses B), die bedingte Wahrscheinlichkeit des Ereignisses B gegeben Veranstaltung A ist einfach der Wahrscheinlichkeit des Ereignisses B, das ist P(B). P(A und B) = P(A)P(B|A).
Was bedeutet hiervon bedingt unabhängig?
Mit anderen Worten, und sind bedingt unabhängig gegeben, wenn und nur dann gegeben, wenn bei Kenntnis, die eintritt, die Kenntnis, ob eintritt, keine Information über die Eintrittswahrscheinlichkeit liefert, und die Kenntnis, ob eintritt, keine Information über die Eintrittswahrscheinlichkeit. auftreten.
Bedeutet Unabhängigkeit bedingte Unabhängigkeit?
3 Antworten. Unabhängigkeit macht nicht implizieren bedingte Unabhängigkeit : zum Beispiel, unabhängig Zufallsvariablen sind selten unabhängig bedingt auf ihre Summe oder auf ihr Maximum.
Empfohlen:
Was sind die vier Rahmenaktivitäten, die in der Extremprogrammierung zu finden sind?

9. Was sind die vier Rahmenaktivitäten im Extreme Programming (XP)-Prozessmodell? Analyse, Design, Codierung, Test. Planung, Analyse, Design, Codierung. planen, analysieren, codieren, testen. planen, designen, codieren, testen
Wie aktiviere ich die bedingte Formatierung in Excel?
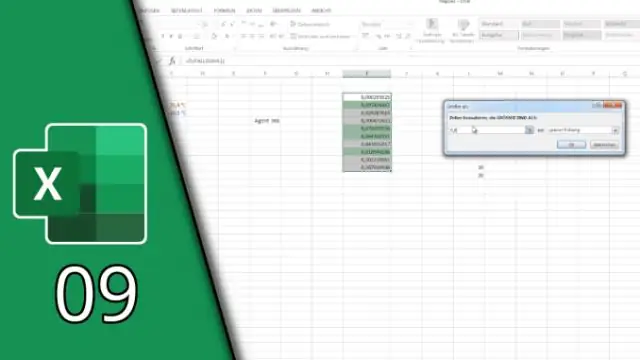
So erstellen Sie eine Regel zur bedingten Formatierung: Wählen Sie die gewünschten Zellen für die Regel zur bedingten Formatierung aus. Klicken Sie auf der Registerkarte Start auf den Befehl Bedingte Formatierung. Bewegen Sie die Maus über den gewünschten bedingten Formatierungstyp und wählen Sie dann die gewünschte Regel aus dem angezeigten Menü aus. Ein Dialogfeld wird angezeigt
Was ist eine bedingte Wahrscheinlichkeitsfunktion?
Bedingte Wahrscheinlichkeit ist die Wahrscheinlichkeit, dass ein Ereignis in irgendeiner Beziehung zu einem oder mehreren anderen Ereignissen auftritt. Beispiel: Ereignis A ist, dass es draußen regnet und es heute mit einer Wahrscheinlichkeit von 0,3 (30 %) regnet. Ereignis B ist, dass Sie nach draußen gehen müssen, und das hat eine Wahrscheinlichkeit von 0,5 (50%)
Was ist bedingte Ausführung in ARM?

GRUNDLAGEN DES ARM-PROZESSORS Die bedingte Ausführung steuert, ob der Kern einen Befehl ausführt oder nicht. Wenn sie übereinstimmen, wird die Anweisung ausgeführt; andernfalls wird die Anweisung ignoriert. Das Bedingungsattribut wird an die Anweisungsmnemonik angehängt, die in die Anweisung kodiert ist
Wie berechnet man die bedingte Wahrscheinlichkeit?

Die Formel für die bedingte Wahrscheinlichkeit wird aus der Wahrscheinlichkeitsmultiplikationsregel abgeleitet, P(A und B) = P(A)*P(B|A). Sie können diese Regel auch als P(A∪B) sehen. Das Unionssymbol (∪) bedeutet „und“, wie in Ereignis A passiert und Ereignis B passiert
