
Inhaltsverzeichnis:
- Autor Lynn Donovan donovan@answers-technology.com.
- Public 2023-12-15 23:42.
- Zuletzt bearbeitet 2025-01-22 17:14.
Implementieren eines binären Suchbaums (BST) in Java
- Der linke Teilbaum eines Knotens enthält nur Knoten mit Schlüsseln kleiner als der Schlüssel des Knotens.
- Der rechte Teilbaum eines Knotens enthält nur Knoten mit Schlüsseln, die größer als der Schlüssel des Knotens sind.
- Der linke und der rechte Teilbaum müssen ebenfalls jeweils a. sein Binärer Suchbaum .
- Es dürfen keine doppelten Knoten vorhanden sein.
Die Frage ist auch, wie die binäre Suche in Java implementiert wird.
Sehen wir uns ein Beispiel für die binäre Suche in Java an, bei dem wir ein Element aus einem Array mithilfe von Rekursion durchsuchen
- Klasse BinarySearchExample1{
- public static int binarySearch(int arr, int zuerst, int zuletzt, int key){
- if (letzter>=erster){
- int mid = erster + (letzter - erster)/2;
- if (arr[mid] == Taste){
- Rückkehr Mitte;
- }
Zweitens, wo verwenden wir den binären Suchbaum? Binärer Suchbaum - Gebraucht in vielen Suche Anwendungen, bei denen ständig Daten ein- und austreten, wie z. B. die Karte und Satzobjekte in Bibliotheken vieler Sprachen. Binär Raumaufteilung - Gebraucht in fast jedem 3D-Videospiel, um zu bestimmen, welche Objekte gerendert werden müssen.
Wie werden binäre Bäume gebildet?
Erstellung eines Binärbaums mit Rekursion
- Lesen Sie eine Daten in x.
- Weisen Sie einem neuen Knoten Speicher zu und speichern Sie die Adresse im Zeiger p.
- Speichern Sie die Daten x im Knoten p.
- Erstellen Sie rekursiv den linken Teilbaum von p und machen Sie ihn zum linken Kind von p.
- Erstellen Sie rekursiv den rechten Teilbaum von p und machen Sie ihn zum rechten Kind von p.
Was ist die Komplexität der binären Suche?
Binäre Suche läuft in der schlechtesten logarithmischen Zeit und führt O(log n)-Vergleiche durch, wobei n die Anzahl der Elemente im Array ist, das O die Big-O-Notation ist und log der Logarithmus. Binäre Suche nimmt konstanten (O(1)) Platz ein, was bedeutet, dass der vom Algorithmus eingenommene Platz für eine beliebige Anzahl von Elementen im Array gleich ist.
Empfohlen:
Wie implementieren Sie die Typ-Ahead-Suche?

Die Typeahead-Suche ist eine Methode zum schrittweisen Suchen und Filtern von Text. Implementieren von Typahead. js Öffnen Sie die Vorlage, die Ihr Suchfeld enthält. Wickeln Sie das Eingabefeld in einen Container mit id=”remote” Geben Sie dem Eingabefeld die Klasse typeahead. Fügen Sie der Vorlage das folgende Skript hinzu:
Wie implementieren Sie die Set-Schnittstelle in Java?
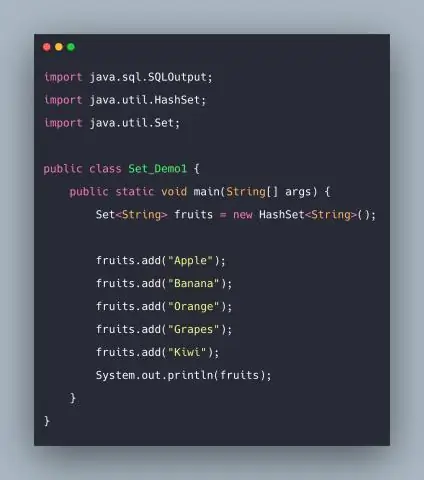
Set in Java Set ist eine Schnittstelle, die Collection erweitert. Es ist eine ungeordnete Sammlung von Objekten, in denen doppelte Werte nicht gespeichert werden können. Grundsätzlich wird Set durch HashSet, LinkedHashSet oder TreeSet (sortierte Darstellung) implementiert. Set verfügt über verschiedene Methoden zum Hinzufügen, Entfernen von Clear, Größe usw., um die Nutzung dieser Schnittstelle zu verbessern
Welche Methode müssen Sie überschreiben, wenn Sie die ausführbare Schnittstelle implementieren?

Eine Klasse, die Runnable implementiert, kann ohne Unterklassen von Thread ausgeführt werden, indem eine Thread-Instanz instanziiert und sich selbst als Ziel übergeben wird. In den meisten Fällen sollte die Runnable-Schnittstelle verwendet werden, wenn Sie nur die Methode run() und keine anderen Thread-Methoden überschreiben möchten
Wie implementieren Sie einen Entscheidungsbaum in Python?
Bei der Implementierung des Entscheidungsbaums durchlaufen wir die folgenden zwei Phasen: Aufbauphase. Verarbeiten Sie den Datensatz vor. Teilen Sie das Dataset aus dem Trainieren und Testen mit dem Python-Sklearn-Paket. Trainieren Sie den Klassifikator. Betriebsphase. Voraussagen machen. Berechnen Sie die Genauigkeit
Wie implementieren Sie eine abstrakte Klasse in Java?

Wenn eine Klasse als abstrakt deklariert ist, kann sie nicht instanziiert werden. Um eine abstrakte Klasse zu verwenden, müssen Sie sie von einer anderen Klasse erben und Implementierungen für die darin enthaltenen abstrakten Methoden bereitstellen. Wenn Sie eine abstrakte Klasse erben, müssen Sie für alle darin enthaltenen abstrakten Methoden Implementierungen bereitstellen
