Video: Sind Diagonalen eines Quadrats Winkelhalbierende?
2024 Autor: Lynn Donovan | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:42
Die Quadrat hat folgende Eigenschaften:
Es gelten alle Eigenschaften einer Raute (wichtig sind hier parallele Seiten, Diagonalen sind Mittelsenkrechte voneinander, und Diagonalen halbieren Winkel ). Es gelten alle Eigenschaften eines Rechtecks (das einzige was hier zählt ist Diagonalen sind deckungsgleich).
Sind davon Diagonalen eines Rechtecks Winkelhalbierende?
Die Diagonalen eines Rechtecks wird nur die halbieren Winkel wenn die Seiten, die sich am. treffen Winkel gleich sind: also nur, wenn die Rechteck ist ein Quadrat. Eine andere Möglichkeit, darüber nachzudenken: die Winkel ist ein Recht- Winkel , und der Winkelhalbierende muss halb rechts herauskommen- Winkel zu den Seiten. Daher die Rechteck muss quadratisch sein.
Man kann sich auch fragen, ob sich die Diagonale des Quadrats gegenseitig halbiert? EIN Quadrat ist ein Sonderfall eines gleichschenkligen Trapezes, Drachen, Parallelogramms, Vierecks, Rechtecks, Raute und Trapezes. Die Diagonalen von a Quadrathalbierende einer Ein weiterer und stehen senkrecht (in der Abbildung oben rot dargestellt). Außerdem sind sie jeden halbieren Paar gegenüberliegender Winkel (blau dargestellt).
Wenn man dies bedenkt, in welchen Vierecken halbieren die Diagonalen die Winkel?
EIN Viereck ist eine Raute, wenn: es ein Parallelogramm ist und ein Paar benachbarter Seiten sind gleich, es ist Diagonalen halbieren einander rechts Winkel , es ist Diagonalen halbieren jeder Scheitelpunkt Winkel.
Was ist die Diagonale des Quadrats?
Diagonalen von a Quadrat . EIN Quadrat hat zwei Diagonalen , die Liniensegmente sind, die gegenüberliegende Scheitelpunkte (Ecken) des Quadrat . Mit anderen Worten, der Punkt, an dem die Diagonalen schneiden (kreuzen), teilt jedes Diagonale in zwei gleiche Teile. Jeder Diagonale teilt die Quadrat in zwei kongruente gleichschenklige rechtwinklige Dreiecke.
Empfohlen:
Sind die Diagonalen des Quadrats gleich?
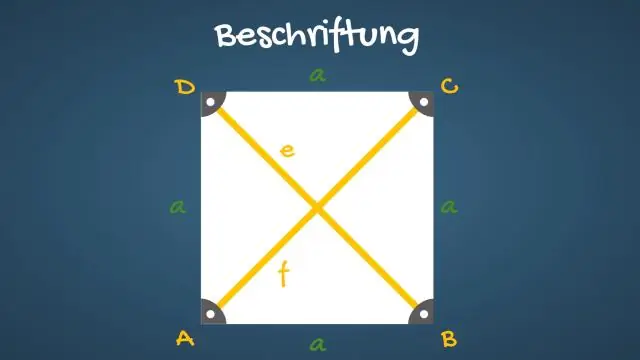
Die Diagonalen eines Quadrats halbieren seine Winkel. Die gegenüberliegenden Seiten eines Quadrats sind parallel und gleich lang. Alle vier Seiten eines Quadrats sind gleich. Die Diagonalen eines Quadrats sind gleich
Kann ich den Bildschirm eines anderen Telefons eines anderen Modells verwenden, um meinen zerbrochenen Bildschirm zu ersetzen?
TU das nicht. Jede Telefongröße ist anders. Und dann sind einige Bildschirme mit vielen Teilen für das Handy eingebettet. Wenn Sie also einen anderen Bildschirm für das Telefon kaufen, verschwenden Sie Ihr Geld
Sind die beiden Diagonalen eines Parallelogramms gleich?
Wenn ein Parallelogramm in zwei Dreiecke geteilt wird, sehen wir, dass die Winkel über die gemeinsame Seite (hier die Diagonale) gleich sind. Dies beweist, dass auch die entgegengesetzten Winkel in einem Parallelogramm gleich sind. Die Diagonalen eines Parallelogramms sind nicht gleich lang
Sind definiert als die Beziehung zwischen den Eigenschaften eines Objekts und den Fähigkeiten eines Agenten, die Hinweise auf die Verwendung eines Objekts geben?
Ein Angebot ist eine Beziehung zwischen den Eigenschaften eines Objekts und den Fähigkeiten des Agenten, die bestimmen, wie das Objekt möglicherweise verwendet werden könnte
Was ist der Nebenläufigkeitspunkt für eine Winkelhalbierende?
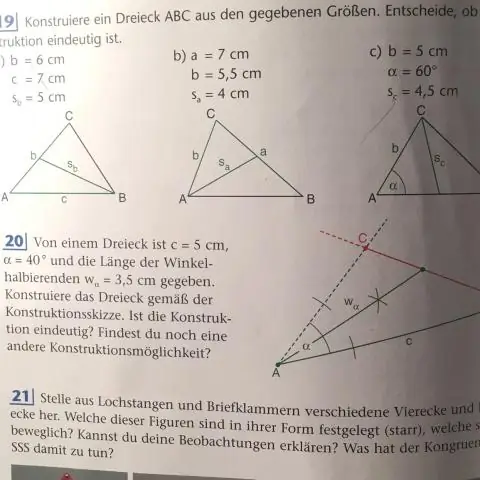
Der Gleichzeitigkeitspunkt der Winkelhalbierenden wird Incenter genannt. Die drei Höhen eines Dreiecks sind gleichzeitig. Der Parallelitätspunkt wird als Orthozentrum bezeichnet. Die drei Mediane des Dreiecks sind gleichzeitig