
- Autor Lynn Donovan [email protected].
- Public 2023-12-15 23:42.
- Zuletzt bearbeitet 2025-01-22 17:14.
Pascals Dreieck ist mehr als nur ein großes Dreieck von Zahlen. Es gibt zwei große Bereiche, in denen Pascals Dreieck ist Gebraucht , in Algebra und inWahrscheinlichkeit / Kombinatorik. Nehmen wir an, Sie haben das Polynom x+1 und möchten es auf einige Potenzen erhöhen, wie 1, 2, 3, 4, 5,.
Außerdem, wie funktioniert das Pascal-Dreieck?
An der Spitze von Pascals Dreieck ist die Zahl 1, die die nullte Reihe bildet. Die erste Reihe (1 & 1) enthält zwei Einsen, die beide durch Addition der beiden darüberliegenden Zahlen links und rechts gebildet werden, in diesem Fall 1 und 0 (alle Zahlen außerhalb der Dreieck sind Nullen). Auf diese Weise werden die Reihen der Dreieck geht unendlich weiter.
Wie verhält sich das Pascalsche Dreieck zu Kombinationen? Kombinationen kann Wiederholung oder keine Wiederholung haben. Die Einträge in Pascals Dreieck sind eigentlich die anzahl von Kombinationen von N nehmen Sie n, wobei N die Zeilennummer ist, beginnend mit N = 0 für die oberste Zeile und n die n-te Zahl in der von links nach rechts gezählten Zeile ist, wobei die n = 0-Zahl die erste Zahl ist.
Welche Jobs verwenden das Pascal-Dreieck?
Heute, pascal S Dreieck wird im Allgemeinen von Designern verwendet, um komplexe und präzise Berechnungen in vielen Aspekten der Mathematik zu erhalten, wird jedoch hauptsächlich in der Algebra und Wahrscheinlichkeit verwendet. Arbeitsplätze so oft verwenden das Dreieck würde bearchitects, Grafikdesigner, Finanzen, Mapping usw.
Wie werden Fibonacci-Zahlen im Pascal-Dreieck verwendet?
Die Zahlen auf Diagonalen des Dreieck hinzufügen Fibonacci-Reihe , Wie nachfolgend dargestellt. Pascal-Dreieck hat viele ungewöhnliche Eigenschaften und eine Vielzahl von Verwendungsmöglichkeiten: Die horizontalen Reihen repräsentieren 11er Potenzen (1, 11, 121, 1331, 14641) für die ersten 5 Reihen, in denen die Zahlen nur einstellige haben.
Empfohlen:
Wozu dient das Schlüsselwort void in Java?

Java-Programmierung/Schlüsselwörter/void. void ist ein Java-Schlüsselwort. Wird bei der Methodendeklaration und -definition verwendet, um anzugeben, dass die Methode keinen Typ zurückgibt, die Methode gibt void zurück. Es ist kein Typ und es gibt keine void-Referenzen/Zeiger wie in C/C++
Wozu dient das XML-Schema?

XML-Schema wird allgemein als XML-Schemadefinition (XSD) bezeichnet. Es wird verwendet, um die Struktur und den Inhalt von XML-Daten zu beschreiben und zu validieren. Das XML-Schema definiert die Elemente, Attribute und Datentypen. Schema-Element unterstützt Namespaces
Wozu dient das Builder-Design-Pattern in Java?
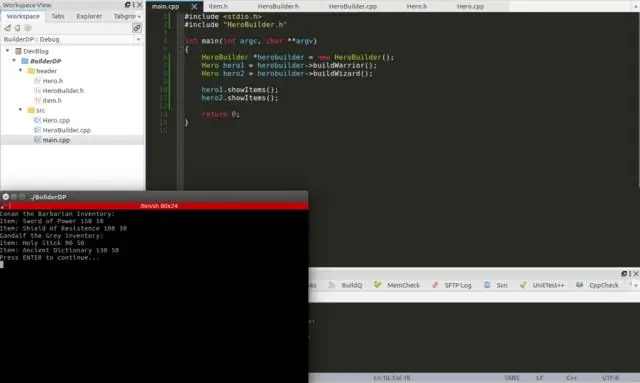
Das Builder-Pattern ist ein Entwurfsmuster, das die schrittweise Erstellung komplexer Objekte mit der richtigen Abfolge von Aktionen ermöglicht. Die Konstruktion wird von einem Director-Objekt gesteuert, das nur den Objekttyp kennen muss, den es erstellen soll
Wozu dient das BrowserModule in Angular?

BrowserModule bietet Dienste, die zum Starten und Ausführen einer Browser-App unerlässlich sind. BrowserModule exportiert CommonModule auch erneut aus @angular/common, was bedeutet, dass Komponenten im AppModule-Modul auch Zugriff auf die Angular-Direktiven haben, die jede App benötigt, wie z. B. NgIf und NgFor
Wozu dient das Hintergrundattribut?
Das background-Attribut kann auch verwendet werden, um den Hintergrund eines HTML-Elements zu steuern, insbesondere Seitenkörper- und Tabellenhintergründe. Sie können ein Bild für den Hintergrund Ihrer HTML-Seite oder Tabelle angeben. Hinweis − Dasbackground-Attribut ist in HTML5 veraltet. Dieses Attribut nicht verwenden
