Video: Warum sind trigonometrische Identitäten beim Lösen von Gleichungen nützlich?
2024 Autor: Lynn Donovan | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:42
Identitäten ermöglichen es uns, komplizierte Ausdrücke zu vereinfachen. Sie sind die grundlegenden Werkzeuge von Trigonometrie zur Lösung trigonometrischer Gleichungen , ebenso wie Factoring, das Finden gemeinsamer Nenner und das Verwenden spezieller Formeln die grundlegenden Werkzeuge von lösen algebraisch Gleichungen.
Was macht dann eine trigonometrische Gleichung zu einer Identität?
In Mathematik, trigonometrische Identitäten sind Gleichheiten, die trigonometrisch Funktionen und gelten für jeden Wert der vorkommenden Variablen, bei denen beide Seiten der Gleichheit definiert sind. Geometrisch sind dies Identitäten mit bestimmten Funktionen eines oder mehrerer Winkel.
Wissen Sie auch, was trigonometrische Gleichungen sind? EIN trigonometrische Gleichung ist irgendwas Gleichung das enthält a trigonometrisch Funktion. Wie in erwähnt Trigonometrisch Identitäten, a trigonometrische Gleichung was für jeden Winkel gilt, heißt a trigonometrisch Identität. Da sind andere Gleichungen , aber das gilt nur für bestimmte Winkel.
Ähnlich kann man sich fragen, wie man trigonometrische Identitäten am einfachsten löst?
SCHRITT 1: Wandeln Sie alle sec, csc, cot und tan in sin und cos um. Das meiste davon kann mit dem Quotienten und dem Kehrwert gemacht werden Identitäten . SCHRITT 2: Überprüfen Sie alle Winkel auf Summen und Differenzen und verwenden Sie die entsprechenden Identitäten sie zu entfernen. SCHRITT 3: Suchen Sie nach Winkelvielfachen und entfernen Sie sie mit den entsprechenden Formeln.
Was ist Sünde 2x gleich?
sin2x =( Sünde x)2=12(1−cos( 2x )).
Empfohlen:
Warum sind Falldiagramme nützlich?
Wenn Sie Unified Modeling Language (UML) verwenden, hilft Ihnen ein Anwendungsfalldiagramm zu verstehen, wie ein Benutzer mit dem von Ihnen entwickelten System interagieren könnte. Und am Ende soll es Ihrem Team helfen, Anforderungen zu definieren und zu organisieren. Stattdessen stellen sie einen allgemeinen Überblick darüber dar, wie Anwendungsfälle, Akteure und Ihr System zusammenhängen
Warum ist eine Schottky-Diode für die Hochfrequenzgleichrichtung nützlich?
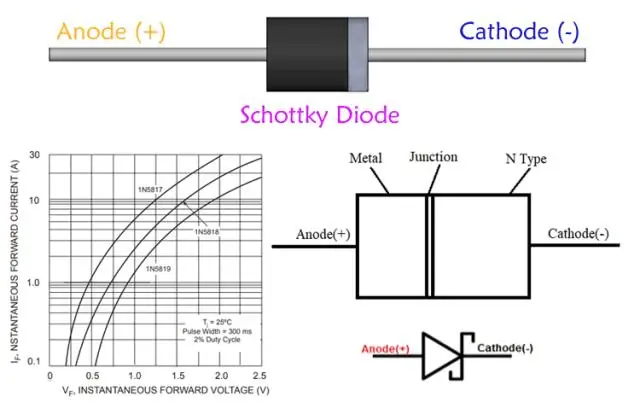
Anwendungen für Schottky-Dioden. Leistungsgleichrichter: Schottky-Dioden werden auch als Hochleistungsgleichrichter verwendet. Ihre hohe Stromdichte und der niedrige Durchlassspannungsabfall bedeuten, dass weniger Energie verschwendet wird, als wenn gewöhnliche PN-Übergangsdioden verwendet wurden. Schottkydioden neigen zu einem hohen Sperrleckstrom
Warum sind Generatoren nützlich?
Generatoren sind seit ihrer Einführung mit PEP 255 ein wichtiger Bestandteil von Python. Mit Generatorfunktionen können Sie eine Funktion deklarieren, die sich wie ein Iterator verhält. Sie ermöglichen es Programmierern, einen Iterator schnell, einfach und sauber zu erstellen. Ein Iterator ist ein Objekt, das iteriert (geschleift) werden kann
Warum sind Suchmaschinen so nützlich?
Im Wesentlichen fungiert eine Suchmaschine als Filter für eine Fülle von verfügbaren Informationen im Internet. Suchmaschinen ermöglichen es Benutzern, nicht nur schnell, sondern auch einfach die Informationen zu finden, die für sie von Interesse oder Wert sind
Warum sind Expertenbewertungen nützlich?
Expertenbewertungen sind eine Technik, die von UX-Forschern verwendet wird, um die Benutzerfreundlichkeit einer Website oder eines anderen digitalen Produkts zu bewerten. Letztendlich sollten beide Techniken zu einer Reihe von priorisierten Empfehlungen zur Verbesserung der Benutzerfreundlichkeit und Benutzererfahrung Ihrer Website führen