Video: Beziehen Sie Ausreißer in die Standardabweichung ein?
2024 Autor: Lynn Donovan | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:42
Standardabweichung ist nie negativ. Standardabweichung ist empfindlich gegen Ausreißer . Ein einzelnes Ausreißer kann die erhöhen Standardabweichung und verzerren wiederum das Bild der Ausbreitung. Bei Daten mit ungefähr gleichem Mittelwert gilt: je größer die Streuung, desto größer die Standardabweichung.
Verwendet die Standardabweichung in dieser Hinsicht Ausreißer?
Wenn ein Wert eine bestimmte Anzahl von ist Standardabweichungen vom Mittelwert entfernt, wird dieser Datenpunkt alsan. identifiziert Ausreißer . Diese Methode kann möglicherweise nicht erkannt werden Ausreißer weil das Ausreißer erhöhen die Standardabweichung . Je extremer die Ausreißer , desto mehr Standardabweichung ist betroffen.
Was gilt auch als Ausreißer? Ausreißer . Der Punkt ganz links in der obigen Abbildung ist beispielsweise ein Ausreißer . Eine bequeme Definition von an Ausreißer ist ein Punkt, der mehr als das 1,5-fache des Interquartilbereichs über das dritte Quartil oder unter das erste Quartil fällt. Ausreißer kann auch auftreten, wenn Beziehungen zwischen zwei Datensätzen verglichen werden.
Wie viele Standardabweichungen sind dementsprechend Ausreißer?
Ein Wert, der außerhalb von 3. liegt Standardabweichungen ist Teil der Verteilung, aber es ist ein unwahrscheinliches oder seltenes Ereignis bei ungefähr 1 von 370 Proben. Drei Standardabweichungen vom Mittelwert ist in der Praxis ein üblicher Cut-off für die Identifizierung Ausreißer in einer Gaußschen oder Gaußschen Verteilung.
Was ist die 1,5 IQR-Regel?
Interquartil Regel für Ausreißer Alles, was wir tun müssen, ist Folgendes: Multiplizieren Sie den Interquartilsabstand ( IQR ) nach der Zahl 1.5 . Hinzufügen 1.5 x ( IQR ) ins dritte Quartil. Jede Zahl darüber ist ein vermuteter Ausreißer. Subtrahieren 1.5 x( IQR ) aus dem ersten Quartil.
Empfohlen:
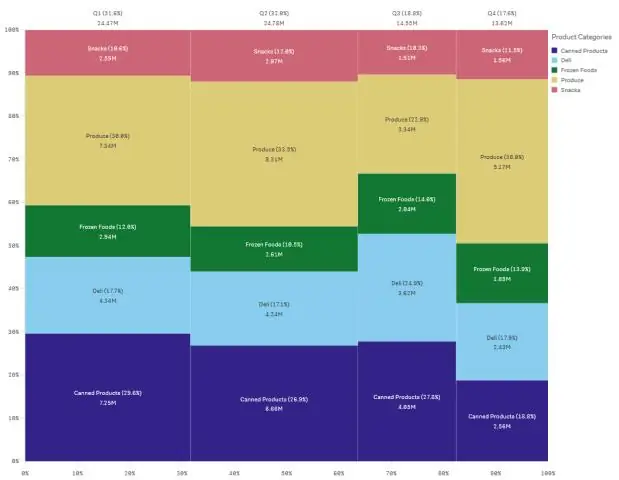
Was ist ein multivariater Ausreißer?
Ein multivariater Ausreißer ist eine Kombination ungewöhnlicher Werte für mindestens zwei Variablen. Beide Arten von Ausreißern können das Ergebnis statistischer Analysen beeinflussen. Ausreißer gibt es aus vier Gründen. Falsche Dateneingabe kann dazu führen, dass Daten Extremfälle enthalten
Was sind Ausreißer in der Datenanalyse?
In der Statistik ist ein Ausreißer ein Datenpunkt, der sich deutlich von anderen Beobachtungen unterscheidet. Ein Ausreißer kann auf Schwankungen in der Messung zurückzuführen sein oder auf experimentelle Fehler hinweisen; letztere werden manchmal aus dem Datensatz ausgeschlossen. Ein Ausreißer kann bei statistischen Analysen schwerwiegende Probleme verursachen
Was ist ein univariater Ausreißer?
Ein univariater Ausreißer ist ein Datenpunkt, der aus einem Extremwert einer Variablen besteht. Ein multivariater Ausreißer ist eine Kombination ungewöhnlicher Werte für mindestens zwei Variablen. Beide Arten von Ausreißern können das Ergebnis statistischer Analysen beeinflussen
Beziehen Sie Ausreißer in die 5-Zahlen-Zusammenfassung ein?
Die fünf Zahlen sind das Minimum, der Wert des ersten Quartils (Q1), der Median, der Wert des dritten Quartils (Q3) und das Maximum. Das Erste, was Ihnen an diesem Datensatz auffallen könnte, ist die Zahl 27. Dies unterscheidet sich stark von den übrigen Daten. Es ist ein Ausreißer und muss entfernt werden
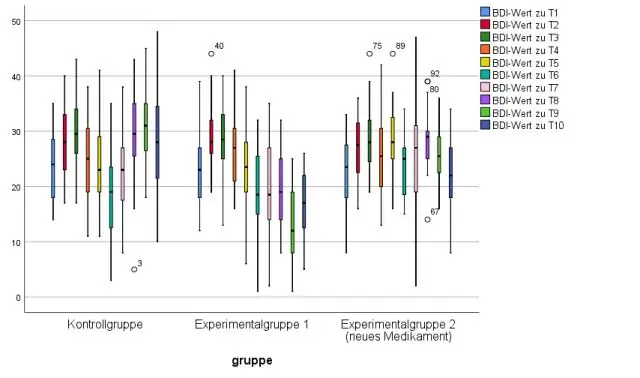
Welcher Graph wird verwendet, um die univariaten Ausreißer anzuzeigen?
1. Univariate Methode. Eine der einfachsten Methoden zur Erkennung von Ausreißern ist die Verwendung von Boxplots. Ein Boxplot ist eine grafische Darstellung zur Beschreibung der Verteilungen der Daten. Boxplots verwenden den Median und das untere und obere Quartil