- Autor Lynn Donovan [email protected].
- Public 2023-12-15 23:42.
- Zuletzt bearbeitet 2025-01-22 17:13.
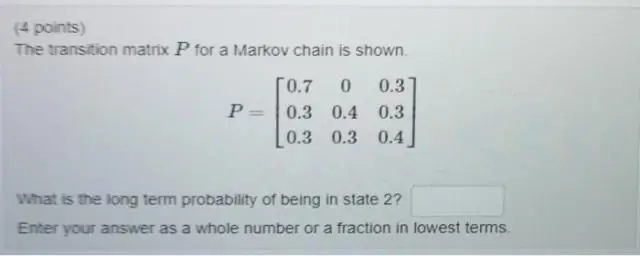
EIN Markov-Kette ist eine stochastische Modell Beschreibung einer Abfolge möglicher Ereignisse, in denen die Wahrscheinlichkeit eines jeden Ereignisses hängt nur von dem Zustand ab, der beim vorherigen Ereignis erreicht wurde.
Vor diesem Hintergrund, was meinen Sie mit Markov-Kette?
EIN Markov-Kette ist ein mathematisches System, das nach bestimmten Wahrscheinlichkeitsregeln Übergänge von einem Zustand in einen anderen erfährt. Das definierende Merkmal von a Markov-Kette ist das egal wie Prozess in seinem gegenwärtigen Zustand angekommen, sind die möglichen zukünftigen Zustände festgelegt.
Man kann sich auch fragen, was ist der Unterschied zwischen der Markov-Kette und dem Markov-Prozess? Die Unterschied zwischen Markovketten und Markovprozessen ist in dem Indexsatz, Ketten eine diskrete Zeit haben, Prozesse haben (normalerweise) kontinuierlich. Zufallsvariablen sind ähnlich wie Meerschweinchen, weder ein Schwein noch aus Guinea. Zufallsvariablen sind Funktionen (die per Definition deterministisch sind).
Anschließend stellt sich die Frage, wofür wird die Markov-Kette verwendet?
Markov-Ketten sind gewöhnt an Berechnen Sie die Wahrscheinlichkeiten des Auftretens von Ereignissen, indem Sie sie als betrachten. Zustände, die in andere Zustände übergehen oder in den gleichen Zustand wie zuvor übergehen. Wir können. Nehmen wir das Wetter als Beispiel: Wenn wir willkürlich Wahrscheinlichkeiten auswählen, wird eine Vorhersage bzgl.
Was ist eine homogene Markov-Kette?
markov - Prozess Graphische-Modell-Graph-Theorie. Ich habe das gelernt Markov-Kette ist ein Graph, der beschreibt, wie sich der Zustand im Laufe der Zeit ändert, und a homogene Markov-Kette ist ein solcher Graph, dass sich seine Systemdynamik nicht ändert.
Empfohlen:
Wie hoch ist die Wahrscheinlichkeit einer GUID-Kollision?
Unter der Annahme einer perfekten Entropiequelle auf jedem Gerät, das zufällige GUIDs generiert, besteht eine 50%ige Kollisionswahrscheinlichkeit, nachdem 2,7e18 zufällige GUIDs generiert wurden. Das sind mehr als 2,7 Millionen Millionen Millionen. Das ist viel
Wie hoch ist die Lebenserwartung einer Sharkbite-Anpassung?

Wie lange halten die SharkBite Fittings? SharkBite-Fittings und PEX-Rohre haben eine 25-jährige Garantie gegen Herstellerfehler, solange der Artikel gemäß den Installationsanweisungen installiert wurde und den lokalen Vorschriften entspricht
Wie macht man die Additionsregel für die Wahrscheinlichkeit?

Additionsregel 2: Wenn zwei Ereignisse, A und B, sich nicht gegenseitig ausschließen, gibt es einige Überschneidungen zwischen diesen Ereignissen. Die Wahrscheinlichkeit, dass A oder B eintritt, ist die Summe der Wahrscheinlichkeit jedes Ereignisses abzüglich der Wahrscheinlichkeit der Überlappung. P(A oder B) = P(A) + P(B) - P(A und B)
Was ist der Unterschied zwischen einer unären Beziehung, einer binären Beziehung und einer ternären Beziehung?

Eine unäre Beziehung liegt vor, wenn beide Teilnehmer der Beziehung dieselbe Entität sind. Zum Beispiel: Fächer können Voraussetzungen für andere Fächer sein. Eine ternäre Beziehung liegt vor, wenn drei Entitäten an der Beziehung teilnehmen
Wie hoch ist die Datenzugriffsgeschwindigkeit einer CD-R?

CD-R-Codierung Verschiedene Kapazitäten Typischerweise bis zu 700 MiB (bis zu 80 Minuten Audio) Lesemechanismus 600-780 nm Wellenlänge (Infrarot und rote Kante) Halbleiterlaser, 1200 Kibit/s (1×) bis 100 Mb/s (56x) Schreiben Mechanismus 780 nm Wellenlänge (Infrarot und roter Rand) Halbleiterlaser Standard Rainbow Books
